Rangkuman Materi Matematika Bangun Ruang Kubus
- Sifat kubus
- Jaring-jaring kubus
- Volume kubus
- Luas permukaan kubus
A. Sifat-sifat Kubus
Kubus merupakan suatu bangun ruang tiga dimensi yang dibatasi oleh enam sisi serupa yang berwujud bujur sangkar.
Kubus juga dikenal dengan nama lain yaitu bidang enam beraturan. Kubus sebetulnya adalah bentuk khusus dari prisma segiempat, sebab tingginya sama dengan sisi alas.
Sifat bangun Kubus:
-Memiliki 6 sisi berbentuk persegi yang memiliki ukuran sama luas
-Memiliki 12 rusuk yang memiliki ukuran sama panjang
-Memiliki 8 titik sudut
-Memiliki 4 buah diagonal ruang
-Memiliki 12 buah bidang diagonal
- Memiliki 6 sisi ;
- Memiliki 12 rusuk ;
- Memiliki 8 titik sudut;
- Memiliki 4 buah diagonal ruang;
- Memiliki 12 buah bidang diagonal;
B. Jaring-jaring Kubus
Jaring jaring yaitu bidang datar berupa gabungan dari bangun datar dan menyusun sebuah bangun ruang.
Jaring-jaring bisa di dapat dengan cara membelah sebuah bangun ruang dengan mengikuti rusuk-rusuknya. jaring-jaring kubus terdiri dari enam buah bangun datar persegi atau bujur sangkar.
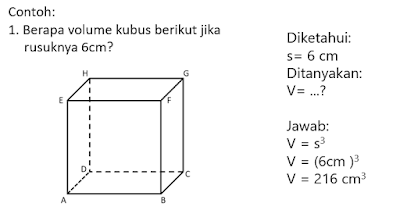
C. Volume Kubus
D. Luas Permukaan Kubus
Luas permukaan suatu benda adalah luas gabungan dari semua sisi permukaan benda tersebut. Keenam sisi kubus sebangun, sehingga untuk mencari luas permukaan kubus kita cukup mencari luas permukaan salah satu sisi kubus lalu mengalikannya dengan enam. Untuk tahu cara mencari luas permukaan kubus, ikuti langkah berikut.
a. Jika Panjang Satu Sisi Diketahui
-Pahami bahwa luas permukaan kubus terdiri dari luas keenam wajah kubus. Karena semua wajah kubus sebangun, kita bisa mencari area satu wajah dan mengalikan dengan 6 untuk mendapatkan total luas permukaan. Luas permukaan dapat ditemukan dengan menggunakan rumus sederhana: 6xs2, "s" merupakan sisi kubus.
-Temukan luas satu sisi kubus. Untuk mencari luas satu sisi kubus, carilah "s" yang merupakan panjang sisi kubus, lalu cari s2. Artinya kita akan mengalikan panjang sisi kubus dengan lebar untuk mencari luasnya. Panjang dan lebar sisi kubus kebetulan sama. Jika salah satu sisi kubus atau "s" adalah 4 cm, maka luas sisi kubus adalah (4 cm)2, atau 16 cm2. Ingatlah untuk menyatakan jawaban dalam satuan persegi.
-Kalikan luas sisi kubus dengan 6. Kita telah mengetahui luas satu sisi kubus, dan sekarang kita akan mencari luas permukaan dengan mengalikan jumlah ini dengan 6. 16 cm2x6 = 96 cm2.
b. Jika Hanya Volume Yang Diketahui
-Temukan volume kubus. Misalnya volume kubus adalah 125 cm3.
-Carilah akar pangkat tiga dari volume. Untuk mencari akar pangkat tiga dari volume, cukup mencari angka yang dapat diakar-pangkatkan tiga, atau gunakan kalkulator. Hasilnya tidak selalu dalam bilangan bulat. Dalam hal ini, 125 adalah sebuah pangkat tiga, dan akar pangkat tiganya adalah 5, karena 5x5x5 = 125. Jadi, "s" atau salah satu sisi kubus, adalah 5.
-Masukkan jawaban ini ke dalam rumus untuk mencari luas permukaan kubus. Sekarang panjang satu sisi kubus diketahui, cukup masukkan ke dalam rumus untuk mencari luas permukaan kubus: 6 x s2. Karena panjang satu sisi adalah 5 cm, cukup masukkan ke dalam rumus seperti ini: 6 x (5 cm)2.
-Hitunglah. Dengan hitungan matematika, 6 x (5 cm)2 = 6 x 25 cm2 = 150 cm2.
Rangkuman diatas dapat dilihat dalam bentuk ebook/flipbook, dan dapat di unduh dalam bentuk dokumen pdf.
ebooknya bisa dilihat disini
Sumber buku:
Buku Siswa SD/MI Kelas VI. Senang Belajar Matematika, edisi revisi. Jakarta: Pusat Kurikulum dan Perbukuan, Balitbang, Kemendikbud, 2018











Posting Komentar